Competing with Einstein for the greatest scientist of the 20th century
He proposes anti-matter not on the basis of physical observation
but because his own mathematical logic tells him that it must exist.
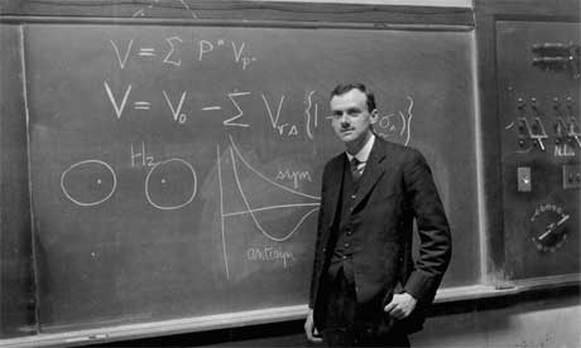
Paul A M Dirac
“In mathematical theories the question of notation, while not of primary importance, is yet worthy of careful consideration, since a good notation can be of great value in helping the development of a theory, by making it easy to write down those quantities or combinations of quantities that are important, and difficult or impossible to write down those that are unimportant….”.
P. A. M. Dirac (1939) [1]
“In mathematical theories the question of notation, while not of primary importance, is yet worthy of careful consideration, since a good notation can be of great value in helping the development of a theory, by making it easy to write down those quantities or combinations of quantities that are important, and difficult or impossible to write down those that are unimportant….”.
P. A. M. Dirac (1939) [1]
